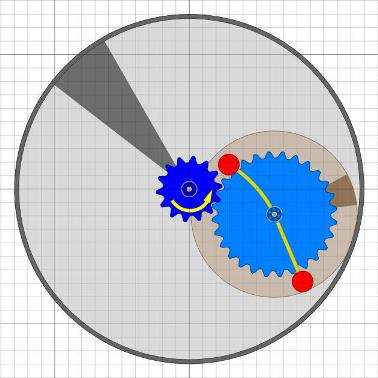
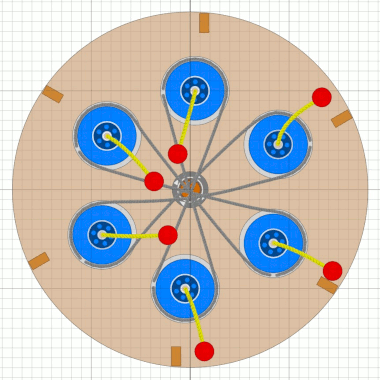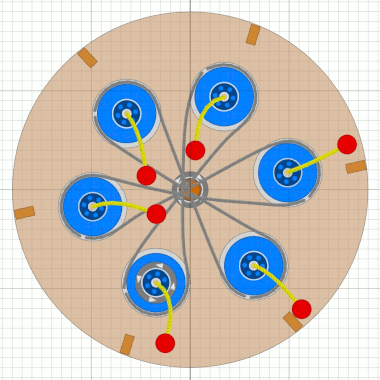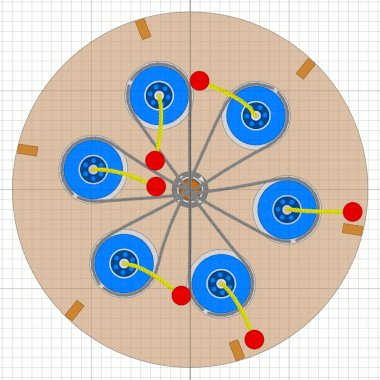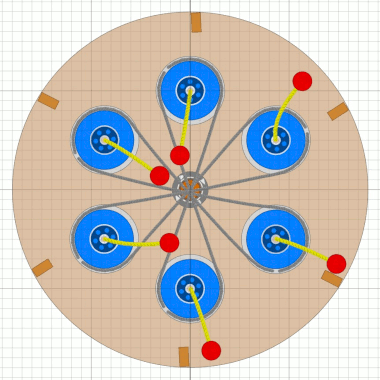
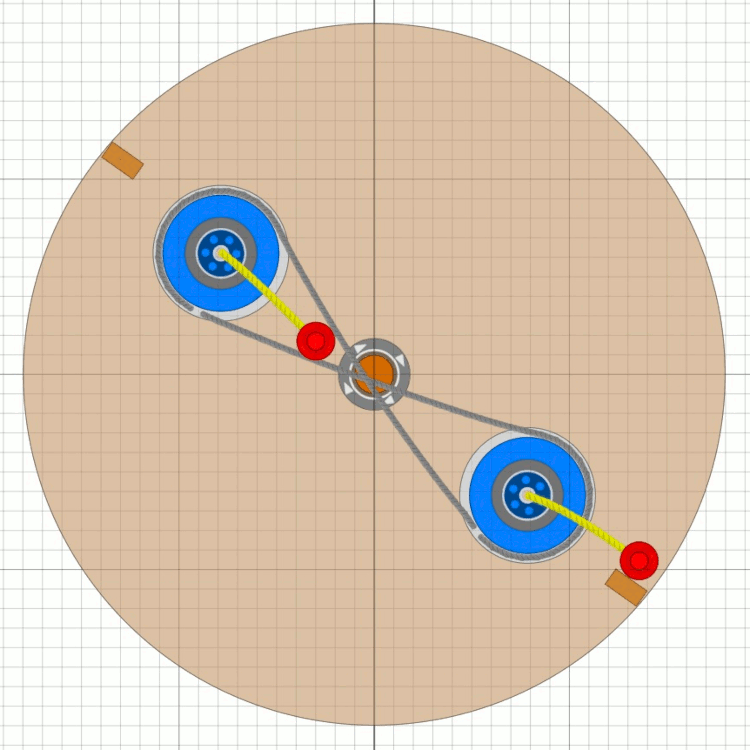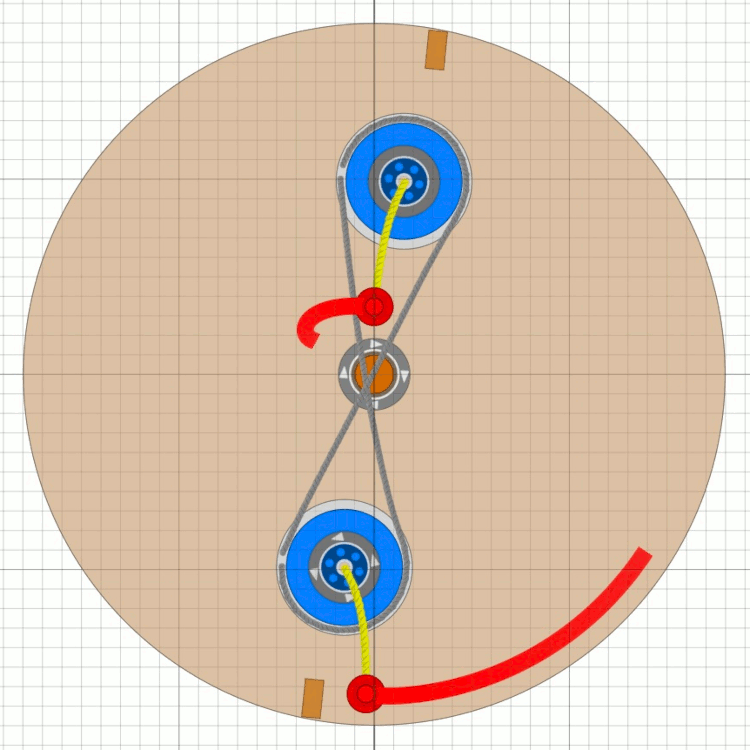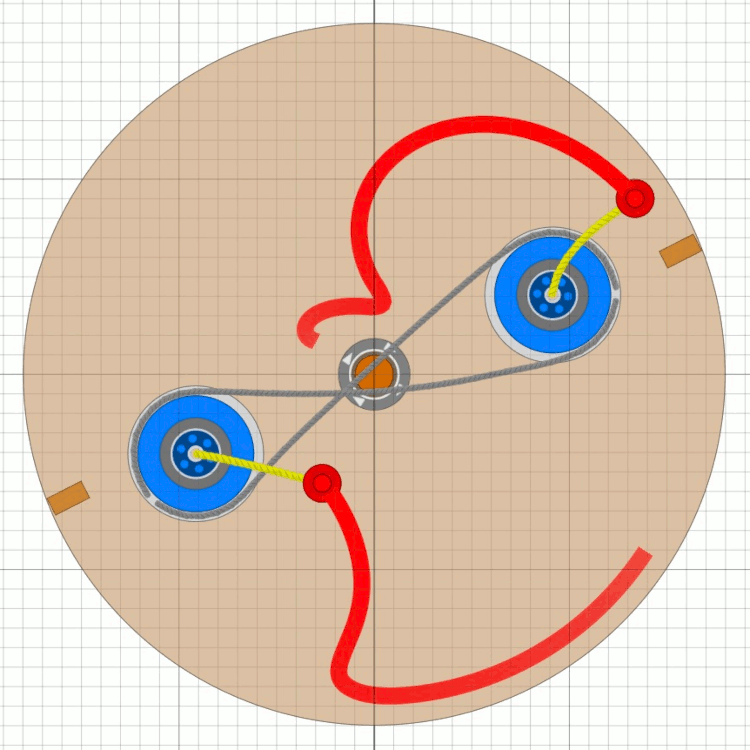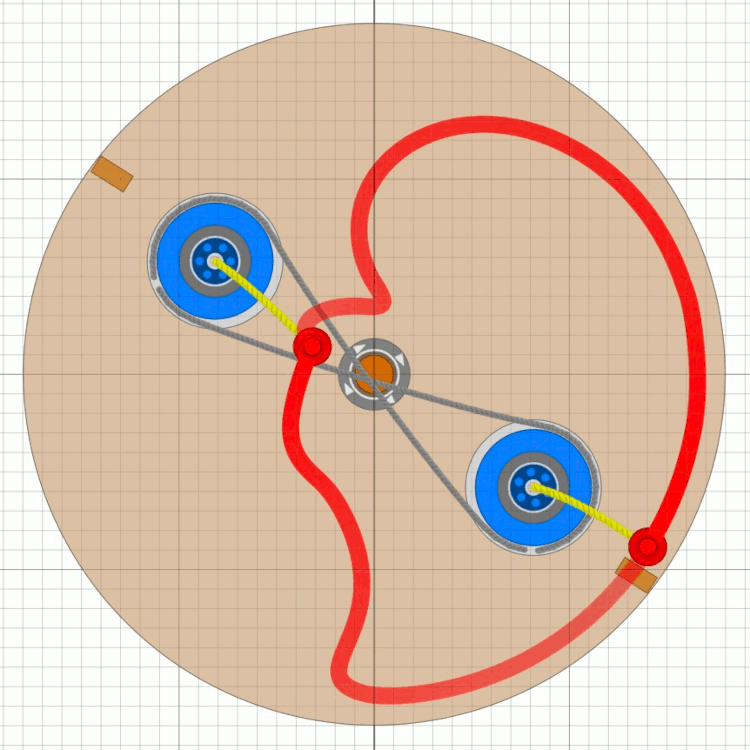
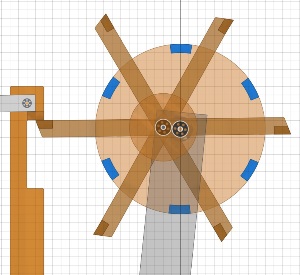
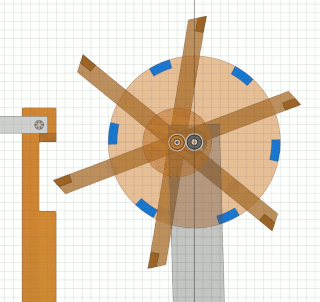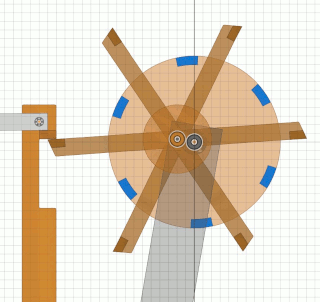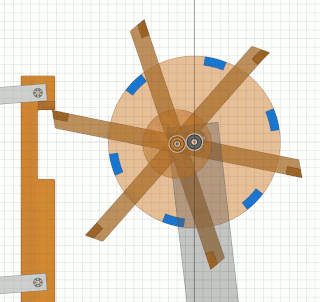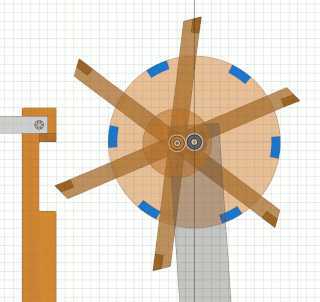
Das Bessler-RadDiese Seiten befassen sich mit einem ungelösten Rätsel in der deutschen Geschichte. Gab es vor über 300 Jahren Maschinen, die nicht nur dauerhaft von sich aus laufen, sondern auch noch Arbeit verrichten konnten ?Mit den folgenden Seiten wird versucht, aus den Überlieferungen eine technische Rekonstruktion des Funktionsprinzips zu erarbeiten und nachzuweisen, dass ein gewisser Herr Bessler damals tatsächlich eine geniale Erfindung gemacht hat. Nachdem sich die Physik seither nicht geändert hat, müsste man solche Maschinen heute besser und leistungsfähiger bauen können. Da die Maschinen wohl rein mechanisch gearbeitet haben, hätten wir damit „erneuerbare Energie” ohne negative Umwelteinflüsse. Die Seiten sind in Form eines Buchs geschrieben, nur mit dem Vorteil, dass auch Animationen möglich sind. Das Buch wird auch immer wieder erweitert und korrigiert, wenn meine Erkenntnisse Fortschritte machen. © 2024/2025 von Alois Zimmermann ( alois-zimmermann@web.de ).
Einleitung EinleitungEin „Perpetuum Mobile” ist nach landläufiger Vorstellung eine Maschine, die sich dauerhaft von sich aus bewegt ohne von aussen Energie zu benötigen. Nach der aktuell anerkannten „etablierten Physik” kann es das aber nicht geben, es würde dem Energie-Erhaltungs-Satz widersprechen.In der Zeit von 1712 bis 1719 hat Johann Bessler jedoch insgesamt vier Maschinen öffentlich vorgeführt, die ununterbrochen mit konstanter Drehzahl laufen und sogar noch Arbeit verrichten konnten. Bessler selbst schrieb in seinem Buch Apologische Poësie auf Seite 45: „Es war darbey gar kein Betrug/ Drum mich auch gar kein Kummer schlug.” Bei mehreren Vorführungen ließ er sich durch sog. Attestate von angesehenen Personen bestätigen, dass keinerlei Energie-Zuführung von aussen gefunden werden konnte. Auch einen Testlauf über 54 Tage in einem nach allen Seiten versiegelten Raum bestand das vierte Rad in Schloss Weissenstein bei Kassel ohne seinen Lauf zu unterbrechen. Es war eine Zeit in der sich die Wissenschaft gerade aus der Alchemie heraus entwickelte und viele Tüftler sog. Perpetua Mobilia zu finden suchten. Um sich die Arbeit zu erleichtern gab es damals nur Wasserräder, Windmühlen oder den Einsatz von Tieren. Viele Versuche das Wasser für die Wasserräder zurück zu führen und mehrmals zu nutzen scheiterten und so reifte die Erkenntnis, dass es so etwas wie einen Energie-Erhaltungs-Satz geben könnte. Anhänger dieser Lehren und Neider standen als Besslers Gegner auf und ließen kein gutes Haar an seiner Erfindung. Das Ende vom Lied: Bessler nahm sein Geheimnis mit ins Grab und über 300 Jahre später ist es immer noch nicht gelüftet. Heute zweifelt (fast) keiner mehr am Energie-Erhaltungs-Satz und so wird allgemein angenommen, dass Bessler ein genialer Betrüger war. Befasst man sich jedoch näher mit seinen Hinterlassenschaften und Schriften so wird einem schnell klar, dass Bessler ein sehr gottesfürchtiger Mensch war und niemals so einen Betrug veranstaltet hätte. - Was also hat Bessler gefunden? - Und wie kann man es mit heutigem Wissen erklären? Für mich als Anhänger einer „Äthertheorie” ist klar: Die Wissenschaft hat sehr viel erreicht und es gibt kaum Bereiche, wo ihre Theorien versagen. Leider wird uns aber meist verschwiegen wie oft mit sog. Ausgleichsfaktoren die Formeln zurecht „gebogen” werden müssen um die richtigen Ergebnisse zu liefern. Meiner Ansicht nach befindet sich die Physik in einer Sackgasse, weil sie nicht von einer „Teilchen”-Physik im Vakuum wegkommt, hin zu einer Schwingungs-Physik im Äther. Die etablierte Physik scheut sich davor die wahre Natur von Teilchen zu ergründen. Sie gibt sich zufrieden mit den ganzen Zirkelschlüssen die in einem Vakuum-Universum notwendig sind - im Prinzip fehlt ihr die Basis. Sollte irgendwann die wahre Natur der Dinge erkannt werden, dann wird die Welt nicht zusammenbrechen. 99,9 Prozent der Formeln werden weiterhin Gültigkeit haben, aber es wird neue Erkenntnisse in astronomischen Zusammenhängen geben. Und was für unser tägliches Leben viel wichtiger ist: Es wird eine Energie-Umwandlung aus der Anziehungskraft (gerichtete Äther-Impuls-Wirkung) möglich sein. Ich selbst kann die ganzen Zusammenhänge mit meiner Äther-Theorie auch noch nicht vollständig erklären. Ich bin aber sicher, dass darin nicht der Energie-Erhaltungs-Satz, sondern der Impuls-Erhaltungs-Satz Priorität haben wird. Vorläufig erkläre ich die Vorgänge im Bessler-Rad gerne mit dem sog. „swing-by”-Manöver von Satelliten um Geschwindigkeit aufzubauen indem sie das Schwere-feld von Planeten ausnutzen. Während ein Satellit ein, zwei oder drei swing-by-Manöver in seinen ersten Jahren durchläuft, laufen im Bessler-Rad wohl fünf bis acht swing-by-Manöver pro Umdrehung ab - und daraus gewinnt es seine Energie. Bessler soll einmal gesagt haben: „Die Maschine gewinnt Kraft aus ihrem eigenen Schwingen heraus”. Nach meiner Vorstellung führen die Gewichte im Bessler-Rad pro Umdrehung mehrere Ein- und Ausschwing-Bewegungen durch (ähnlich swing-by-Manövern) und nutzen dabei gezielt die Fliehkraft und den Pirouetten-Effekt. Wer war Johann Ernst Elias Bessler?Elias Bessler wurde 1681 in der Nähe von Zittau geboren als Kind armer Leute (Zittau in Sachsen im Dreiländereck Deutschland/Polen/Tschechien). Schon in der Schule erkannte ein Lehrer sein Interesse an allerlei mechanischen Spielzeugen, so dass er in die Obhut des Schulleiters genommen wurde und eine für die damalige Zeit gute Schulbildung bekam. Sozial war Bessler wohl kein einfacher Mensch, er hatte mit ziemlicher Sicherheit eine Inselbegabung und würde heute wahrscheinlich in die Kategorie „Asperger Autist” eingeordnet werden.Etwa 50 Jahre nach dem 30-jährigen Krieg und am Ende der kleinen Eiszeit (Maunder-Minimum an Sonnenflecken) war Deutschland damals in Fürstentümer eingeteilt und langsam konnte sich aus der kargen und wirren Zeit auch ein kulturelles Leben entwickeln. Nach der Schule führte Bessler für kurze Zeit ein ausschweifendes Leben, das er aber mit seinem festen Glauben nicht vereinbaren konnte. So ging er als Handwerksbursch auf die Walz um Vieles kennen zu lernen. Er wollte nicht nur einen Beruf erlernen, sondern möglichst alle, und blieb meist nur wenige Wochen an einem Ort. Auf seiner Walz durch große Teile Europas (Prag, Wien, Augsburg usw.) fand er auch Unterschlupf in einem Kloster im Welschland (Oberitalien) wo ihm ein Bratenwender auffiel, der auch nach dem Essen weiterlief. Auf die Frage warum man den Bratenwender denn leer noch weiter drehte bekam er die Antwort: „Diesen Bratenwender treibt uns der liebe Herrgott an”. Das interessierte ihn und er wollte die Mechanik dahinter sehen. Durch Mitarbeit im Kloster konnte er sich einen Einblick verdienen und so wurde er nach ein paar Wochen in den Raum hinter der Küche geführt. Dort war wohl einiges an Mechanik am werkeln und Bessler prägte sich so viel wie möglich ein. Von da an wollte er so eine selbst laufende Maschine bauen, die aber kompakt und beweglich sein sollte um sie dahin zu schieben, wo ein Antrieb gebraucht wurde. Zehn Jahre lang tüftelte er daran, baute unzählige Modelle, sparte sich vieles vom Munde ab und war des öfteren am verzweifeln. Im Jahre 1712 kam dann der Durchbruch, seine erste Maschine drehte sich von selbst. Er baute dann wohl ein besseres Modell, insbesondere war ihm wichtig die innere Funktion zu verdecken, und am 6. Juni 1712 präsentierte er sein sog. „erstes Rad” der Öffentlichkeit auf dem Nickelsberg in Gera. Ihm war klar, dass er da etwas ganz besonderes gefunden hatte und wollte das Wissen für eine größere Summe verkaufen um sich endlich ein besseres Leben leisten zu können. Leider ohne Erfolg. Immer wieder musste er sein Rad zerschlagen (Gera und Draschwitz), in eine andere Stadt ziehen und von vorne anfangen. Nach seinem beschwerlichen Leben wollte er sein Geheimnis keinesfalls preis-geben ohne einen angemessenen Gegenwert zu erhalten. Er fing an Bücher zu schreiben um bekannt zu werden und möglichst einen potenten Käufer zu finden. Im „Gründlichen Bericht” beschrieb er sein drittes Rad und stellte verschiedene Einsatzmöglichkeiten für seine Maschine vor. In späteren Schriften erzählte er einzelne Begebenheiten aus seinem Leben, beklagte sich über seine Gegner und streute auch verschlüsselte Hinweise ein um die Schriften interessanter zu machen und evtl. seine Rechte an der Erfindung abzusichern. In seinen Wanderjahren hatte er nicht nur Handwerksberufe, sondern auch Sprachen und allerlei Geheimkünste erlernt. So rettete er einmal einen Rabbiner vor dem Ertrinken und der ließ ihn dafür über ein Jahr lang bei sich wohnen und lehrte ihn Hebräisch sowie die Kabbala. Auch zu Logen-Wissen soll er Zugang bekommen haben. Bessler hatte also ein immenses Geheimwissen und wusste es zu nutzen um einzelne Details seiner Maschinen verschlüsselt schon zu ver-öffentlichen. Er war sehr misstrauisch und fürchtete, dass ein anderer Tüftler eine ähnliche Erfindung vorstellen könnte und als erster dafür den Ruhm abräumte. Er hätte dann die Verschlüsselung aufgedeckt um klar zu machen, dass er schon eher zum Durchbruch kam und ihm die Ehre gebührte. Bessler nutzte auch gerne die Gelehrtensprache Latein und latinisierte damit seinen Namen BESSLER per ROT12/ROT13-Verschiebung in ORFFYRE bzw. Orffyreus. Ab ca. 1714 nahm er auch zwei weitere Vornamen an, Johann und Ernst, weil er wohl ein zweites E und ein W für seine Codierungen brauchte. (Durch die ROT12-Verschiebung der Buchstaben entsteht aus dem J ein W und es wird auch angenommen, dass er das W wiederum als VV sehen wollte, was wiederum als 55 gedeutet werden kann. Und 5 ist ziemlich sicher eine Schlüsselzahl in seinen Rädern.) Für Bessler war das J (W) wohl so wichtig, dass er Johann zu seinem Haupt-Vornamen machte. Mehr Details zu Besslers Leben kann man in www.besslerrad.de finden. Die vier öffentlich vorgeführten RäderWie schon gesagt hat Bessler sein erstes Rad in Gera vorgestellt. Schon bald standen aber Zweifler und Neider auf, die ihn als Betrüger beschimpften, nur weil er die Funktion seines Rades aus guten Gründen nicht preisgeben wollte. Das ging so weit, dass er das Rad zerstörte und aus der Gegend weg zog, als die Anfeindungen zu massiv wurden und er schon gesundheitliche Probleme bekam. Insbesondere drei Gegner machten ihm sehr zu schaffen: ein Student Christian Wagner (später Advokat und Mathematiker in Leipzig), der Hofmodellbaumeister Andreas Gärtner (Illusionist), der nicht zulassen konnte, dass ein anderer besser war und Johann Gottfried Borlach, ein sächsischer Bergrat.Erstes Rad: auf dem Nickelsberg in Gera am 6. Juni 1712 Zweites Rad: in Draschwitz im Herbst 1713 Drittes Rad: in Merseburg vor den Pfingstferien 1715 Viertes Rad: auf Schloss Weissenstein bei Kassel 1716/1717 Die Schriften BesslersBessler hat insgesamt vier Schriften (Drucke) und eine Skizzensammlung hinterlassen. Mit seinen Drucken wollte er seine Erfindung bekannt machen um einen Käufer zu finden. Sein erstes Werk war der Druck „Gründlicher Bericht” in dem er sein drittes Rad beschrieben hat. Dann kamen die „Apologische Poësie” und die „Poëtische Apologie”, die er in Versform verfasste und mit denen er sich gegen seine Gegner rechtfertigte, gleichzeitig aber auch sein karges Leben und sein Suchen in verschiedenen Etappen zu Papier brachte. Nachdem sein viertes Rad den Lauf von 54 Tagen in einem versiegelten Raum bestanden hatte, schrieb er das letzte große Werk „Das Triumphierende”, wieder in Prosa, aber in zwei Spalten in Deutsch und in Latein. In Archiven sind auch Briefwechsel mit Gelehrten, Fürsten und Ämtern sowie Zeitungsinserate erhalten. Nach seinem Tod wurde dann noch eine Loseblattsammlung von Skizzen entdeckt, die heute als „Maschinen-Traktate” bekannt ist. Sie umfasst ca. 140 Skizzen von Rädern, die sich von selbst drehen sollten, das Geheimnis ist aber wenn überhaupt nur sehr verschlüsselt enthalten. Wenn Bessler seine Maschine hätte verkaufen können, dann hätte er die Blätter wohl zum Unterricht für Interessierte genutzt.Gründlicher Bericht: gedruckt im Dezember 1715 - - -> download Apologische Poësie (1.Theil): 1716 - 1717 - - -> download Poëtische Apologie (2.Theil): 1716 - 1717 - - -> download Das Triumphierende: gedruckt zu Kassel im Oktober 1719 - - -> download Maschinen-Traktate: Loseblatt-Sammlung - - -> download Im Folgenden gebe ich Referenzen zu diesen Schriften verkürzt an, z.B.: GB Seite 30 oder noch kürzer GB 30 für Seite 30 im Gründlichen Bericht, AP für Apologische Poësie, PA für Poëtische Apologie, DT für Das Triumphierende und MT für Maschinen-Traktate. Ausserdem ist zu beachten, dass hier Drucke eingescannt wurden. Es gibt also verschiedene Originale und daher auch unterschiedliche Qualitäten der Digitalisierung. Hier noch ein paar Kostproben aus den verschiedenen Schriften:
Die rechte Spalte zeigt denselben Text in Latein. Die Skizze Nr. 13 in den Maschinentraktaten ist spiegelbildlich gezeichnet und hat wohl eine gewisse Bedeutung, besonders die letzte Aussage. No:13. Ist eine neue Gewichts=Invention, wobei keine Riemen oder Kette,
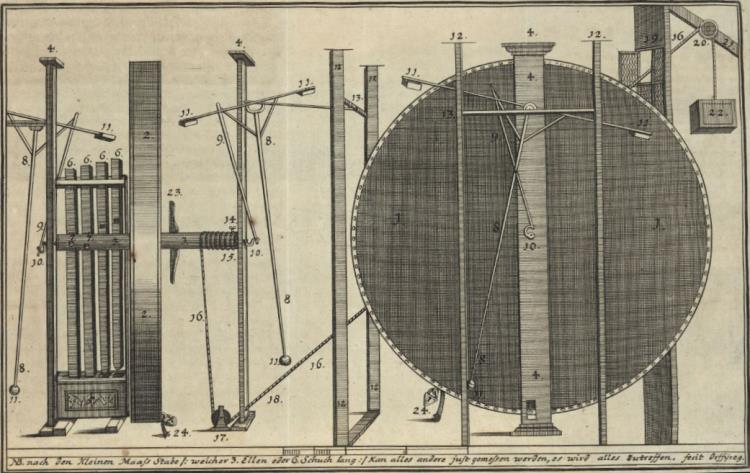
Das erste Rad von GeraVom ersten Rad ist nur sehr wenig überliefert und das auch noch nicht eindeutig. Im „Gründlichen Bericht” GB schreibt Bessler auf S. 6 unten, dass „das erste Modell seines Perp. ac per se Mobilis, so drittehalb Leipziger Ellen in Diametro und 4 Zoll in der Dicke gehabt, am 6. Junii nur gedachten 1712=ten Jahres zum ersten mahle, .” öffentlich vorgestellt wurde.
Besslers Hinweise auf das erste Rad: GB Seite 6 unten: Durchmesser 2½ Ellen, Dicke 4 Zoll AP Seite 44: Durchmesser 2½ Schuh, selbstanlaufend DT Seite 18: Rad von Draschwitz war wie das Rad von Gera, nur größer Das zweite Rad von DraschwitzFür mich lieferte Gottfried Teuber, Hofdiakon und Magister in Zeitz, die aussagekräftigste Beschreibung eines Bessler-Rades. Er war nicht nur ein hoher Geistlicher und Gelehrter, sondern er hatte auch ein ausgeprägtes Interesse an technischen Apparaten.Hier der Bericht von Gottfried Teuber (1656-1731) zum Rad von Draschwitz: „Es handelt sich um ein hohles Holzrad, 10 Fuß im Durchmesser und 6 Zoll dick. Es wird von dünnen Holzbrettern bedeckt, die den inneren Mechanismus verbergen. Die Achse ist auch aus Holz und ragt auf beiden Seiten einen Fuß über das Rad hinaus. Sie hat Zähne, die 3 Stampfhölzer bewegen, ähnlich wie man sie in Stampfmühlen findet. Diese Stampfhölzer sind recht schwer, und sie werden unablässig angehoben und wieder fallen gelassen. Die eisernen Achszapfen drehen sich in offenen Lagern, so dass man einen Betrug durch äussere Energiezuführung ausschließen kann. Ich hatte mit dem Erfinder ein Treffen vereinbart. Als wir uns der Maschine näherten, konnte ich sehen, dass das Rad mit einem dicken Seil arretiert war. Sobald das Seil gelöst wurde, begann sich die Maschine mit großer Kraft zu drehen. Für längere Zeit hat sie ihr Tempo weder beschleunigt noch verlangsamt. Um sie wieder anzuhalten, war große Kraft erforderlich.”
Besslers Hinweise auf das zweite Rad: AP Seite 47, GB Seiten 7 und 8 Das dritte Rad von MerseburgDas dritte Rad von Merseburg ist in einem Stich von Bessler veröffentlicht im „Gründlichen Bericht” vom Dezember 1715. Dieses Rad lief nicht von selbst an, konnte dafür aber mit wenig Kraft in beide Richtungen in Bewegung gesetzt werden und hatte dann eine Drehzahl von ca. 40 U/min.Für die damalige Zeit wäre es eine interessante Arbeitsmaschine auf Baustellen oder im Bergbau gewesen, da es ca. 35 Kilogramm hochziehen und auch definiert absenken konnte. Auch für mich war es lange Zeit der Favorit. Heute würde man ein Bessler-Rad aber zur Stromerzeugung einsetzen und da würde das einfachere und bei gleicher Grösse wohl leistungsfähigere zweite Rad genügen.
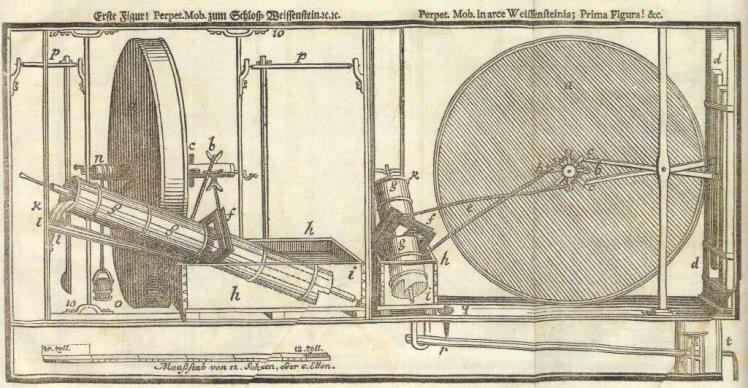
Legende: „NB: nach den Kleinen MaßStabe /: welcher 3.Ellen oder 6.Schuch lang :/ kan alles andere just gemessen werden, es wird alles zutreffen. fecit Orffyreus.” Der „Gründliche Bericht” befasst sich fast ausschließlich mit dem Rad von Merseburg und den sog. Attestaten, also Testvorführungen vor honoren Personen, die bestätigten, dass kein Betrug gefunden werden konnte. Hinweise auf Maße und Funktion finden sich auf den Seiten 9, 10, 12, 16, 19, 27, 29, und 32. Das vierte Rad von Weissenstein bei KasselMit dem vierten Rad von Kassel wollte Bessler noch besser auf die Bedürfnisse der damaligen Zeit eingehen. Neben den bekannten Eigenschaften vom dritten Rad war auch noch eine archimedische Schraube (Wasserpumpe) integriert, evtl. um die beliebten Wasserspiele bei Hofe zu betreiben. Das Rad konnte aber auch ohne diese Pumpe betrieben werden, da dieses Rad vom 12. November 1717 bis zum 4. Januar 1718 insgesamt 54 Tage lang in einem versiegelten Raum im Dauerbetrieb laufen musste. Da es in diesem Winter sicher sehr kalt war (Maunder-Minimum, kleine Eiszeit) hätte das mit dem Wasser wohl nicht so lange funktioniert auch wenn Bessler damals schon wusste wie er das Wasser behandeln musste, dass es nicht einfriert. Zu diesem langen Testlauf kam es übrigens aufgrund einer Wette mit seinen Widersachern. Den sehr hohen Wett-Einsatz hat er aber wohl nie bekommen.
Interessant sind hier auch die Stampfhölzer. Wenn wir zurückgehen zum dritten Rad, dann sehen wir vier Stampfer. Lange hatte ich hier die falsche Vorstellung, dass die Pumpe für fehlende Stampfer-Impulse sorgen musste, bis ich kapierte, dass durch die langsamere Drehzahl jeder Stampfer viermal pro Umdrehung gehoben werden konnte. Es ist gut dokumentiert, dass die Drehzahl vom Leerlauf mit 26 U/min bei Belastung auf ca. 20 U/min zurückging. Interessant ist auch, dass pro Rad-Umdrehung „etwa” 8 Geräusche in dem Rad zu hören waren auf der Seite zu der hin sich das Rad drehte. Das Rad hatte einen Durchmesser von 12 Rheinländische Fuß (ca. 3,72 m), war 15 bis 18 Zoll breit (etwa 40 - 45 cm) und hatte eine Achse aus Holz von 6 Fuß Länge (1,8 - 1,9 m) mit Lagerzapfen, die etwas dünner als ein Zoll und leicht konisch waren. Der Durchmesser der Holzachse war im Durchschnitt 8 Zoll (ca. 20 cm). Mit einem Seil um diese Achse konnte es etwa einen Zentner heben oder langsam absenken. Unter Berücksichtigung der Drehzahl von 20 U/min bei voller Belastung kann man die Leistung zu etwa 100 Watt berechnen: P = m * g * r * ω = 50 * 9,81 * 0,1 * 2π * (20/60) = 102,7 Watt. Jeder der zwei Stampfer hatte ein Gewicht von 20 - 30 Kilogramm und wurde pro Sekunde fast zwei mal angehoben. Besslers Hinweise auf das vierte Rad: DT ab Seite 19 Begriffsbestimmungen
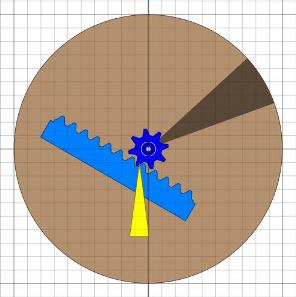
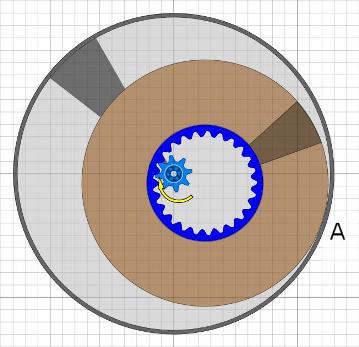
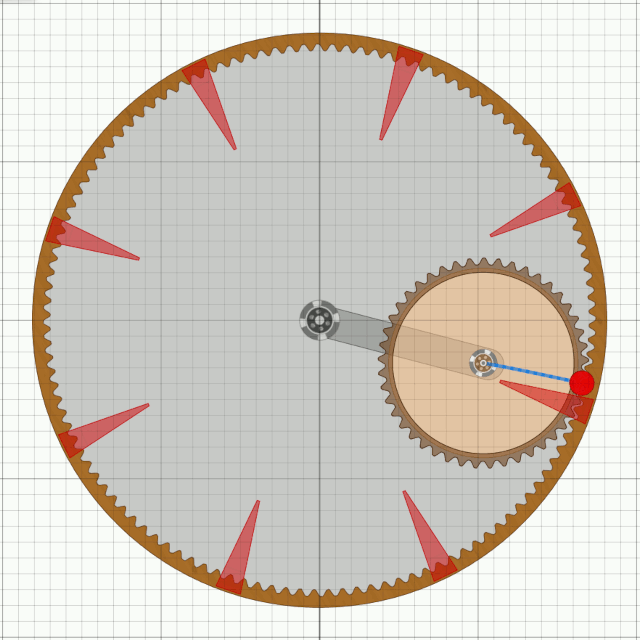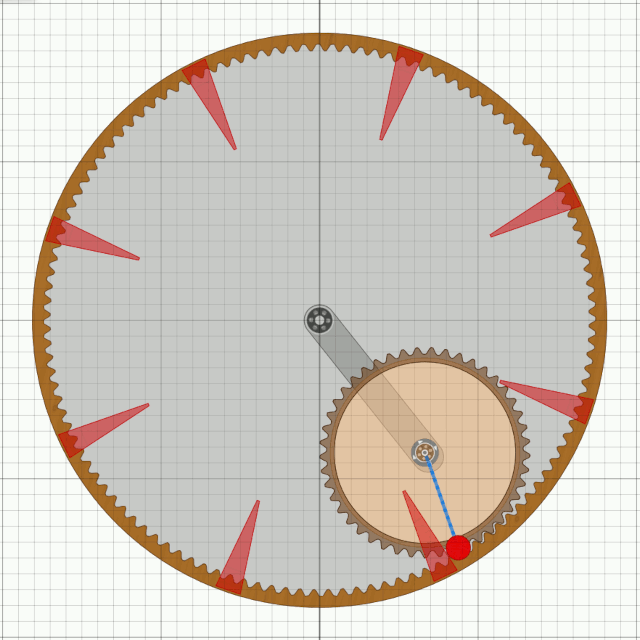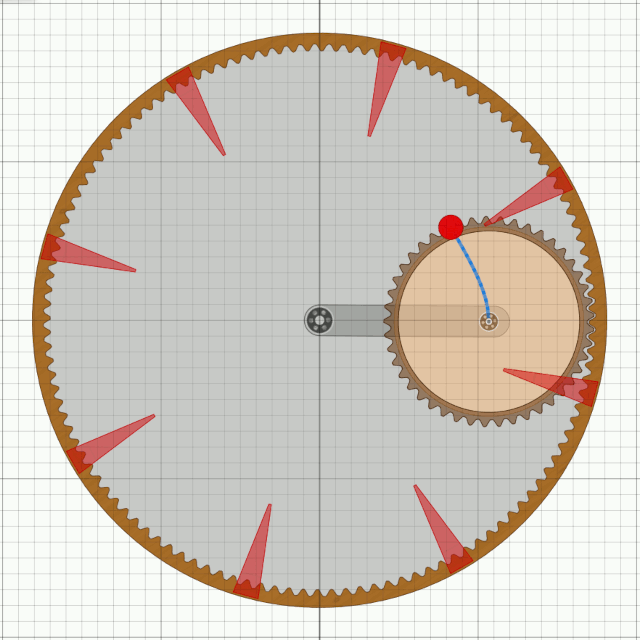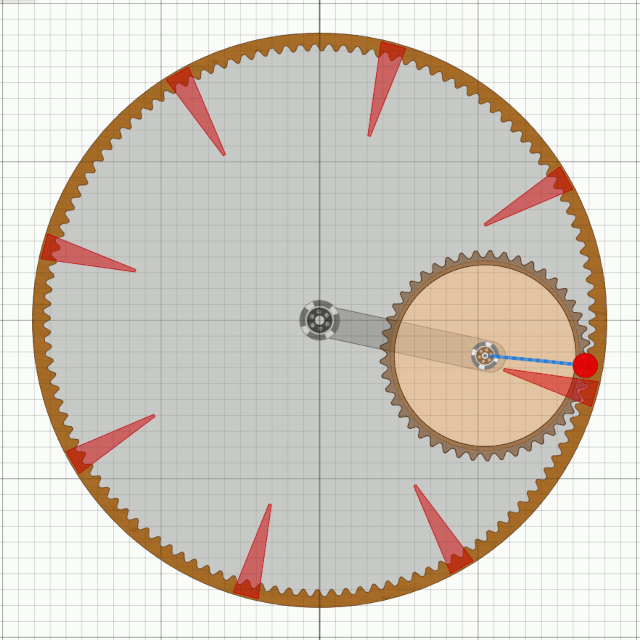
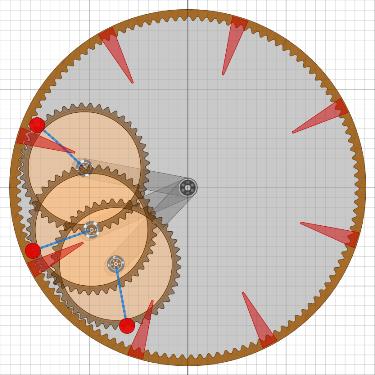
Das UnwuchtsystemIrgendwo hat Bessler einmal geschrieben: „...dass meine Unwucht anders ist“.Nachdem ich ca. 7 Jahre lang mit Hilfe von Algodoo und auch einigen realen Experimenten nach dem Prinzip der Bessler-Räder gesucht habe und schon ziemlich frustriert war, kam mir ein neuer Ansatz in den Sinn. Wieder hat es lange gedauert bis ich die Zusammenhänge so einigermaßen durchschaut habe. Im Nachhinein lässt es sich aber ganz gut erklären.
Wir erinnern uns an die Aussage in AP 20: „Denn diesem Dinge war verliehen/ Es thät sich immer selbst aufziehen:” Jetzt verlegen wir diese Anordnung in ein Rad mit dem linken Zahnrad als Zentrum, dann kann die abrollende Scheibe schon mal nicht mehr wegspringen.
Aktuell kann das Rad keine durchgehende Welle haben, weil diese die innere Scheibe durchstechen und blockieren würde. Dafür gibt es aber eine Abhilfe:
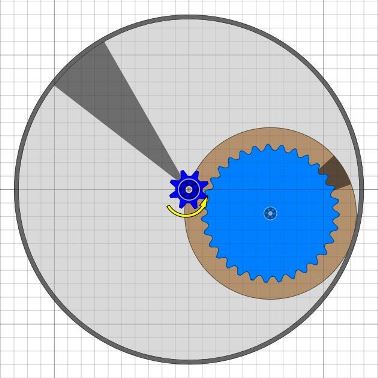
Das wäre ein Weg um eine durchgehende Welle im Bessler-Rad zu ermöglichen. Bessler hat aber doch wahrscheinlich einen anderen Weg gewählt. Er hat wohl die Innenscheiben/-räder kleiner gemacht, so dass sie auf einer Seite ins Rad passten. Ich nenne sie mal Satellitenräder.
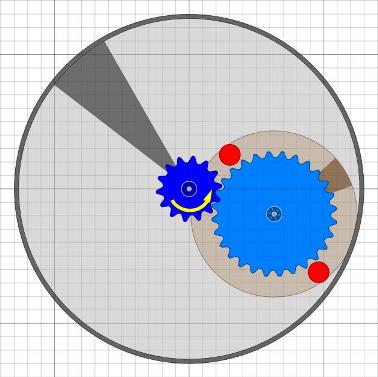
Im nächsten Schritt lösen wir das homogene Satellitenrad auf in eine sehr leichte Scheibe, die nur noch zum Abrollen benötigt wird und zwei separate Gewichte die darauf befestigt sind. Das Ziel ist es nur noch ein Gewicht heben zu müssen. Das andere soll auch während der Hebe-Phase zur Beschleunigung des Rades beitragen.
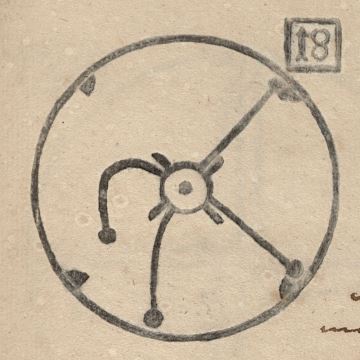
Und da kommt die wohl wichtigste Abbildung in Besslers Maschinentraktaten ins Spiel, MT18.
Durch Anwendung von MT18 auf das Satellitenrad ist das Unwuchtsystem eines Bessler-Rades dann fertig.
„Nicht gezeiget ist woher eigentlich das primum movens kommen sollte.” Das Stampfwerk
Im letzten Kapitel haben wir herausgearbeitet wie wohl das Unwuchtsystem in den Bessler-Rädern
prinzipiell aufgebaut war. Die grundsätzliche Funktion sollte so sein, dass ein Fluggewicht
mit weniger Aufwand angehoben wird als es dann an Energie abgibt, wenn es aussen am Rad wieder nach unten geht. Für mich ist das Stampfwerk vergleichbar mit der Nockenwelle in einem Verbrennungsmotor. Es steuert interne Vorgänge im Rad (Unwuchtsystem) und gibt sogar die nötigen Energie-Impulse dazu, damit die Aktionen auch schnell ausgeführt werden können. Wie allerdings die Mechanik ausgesehen hat, die die Kraft vom Zapfen an der Achse zum Unwuchtsystem im Rad weitergeleitet hat und evtl. sogar noch die Impulsrichtung invertiert hat, das ist noch immer Besslers Geheimnis. Das Geheimnis in der AchseBessler hat sein erstes Rad erst zum Laufen gebracht, nachdem ihn Gott das „Geheimnis in der Achse” hat schauen lassen. Was hat es damit auf sich?
Ich bilanziere mal die Drehmomente und Leistungen am und im Rad: Das Prinzip der ersten RäderObwohl von den ersten Rädern (Gera und Draschwitz) nur wenig überliefert ist, kann ich inzwischen den grundsätzlichen Aufbau einigermaßen nachvollziehen. Die meisten Informationen liefert die Beschreibung von Gottfried Teuber und auch einzelne Verse von Besslers Schriften lassen sich diesen Rädern zuordnen, z.B. AP 81. Der Rest ist Tüfteln, logisch vorgehen und die Maschinentraktate zu Rate ziehen, z.B. MT 13, MT 18, MT 55 und MT 138-141. Sicher ist:
Von mir als sehr wahrscheinlich zusätzlich angenommen:
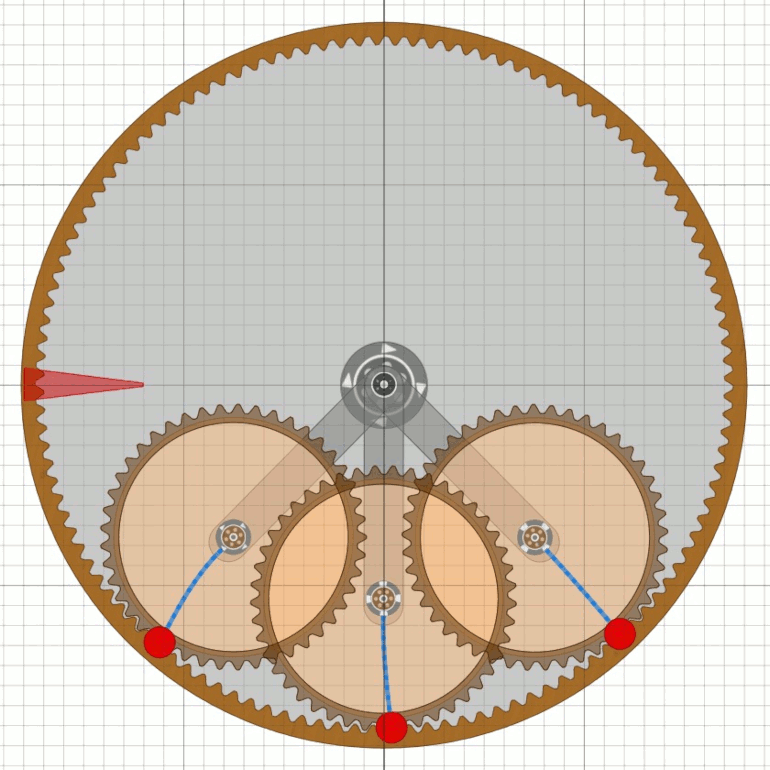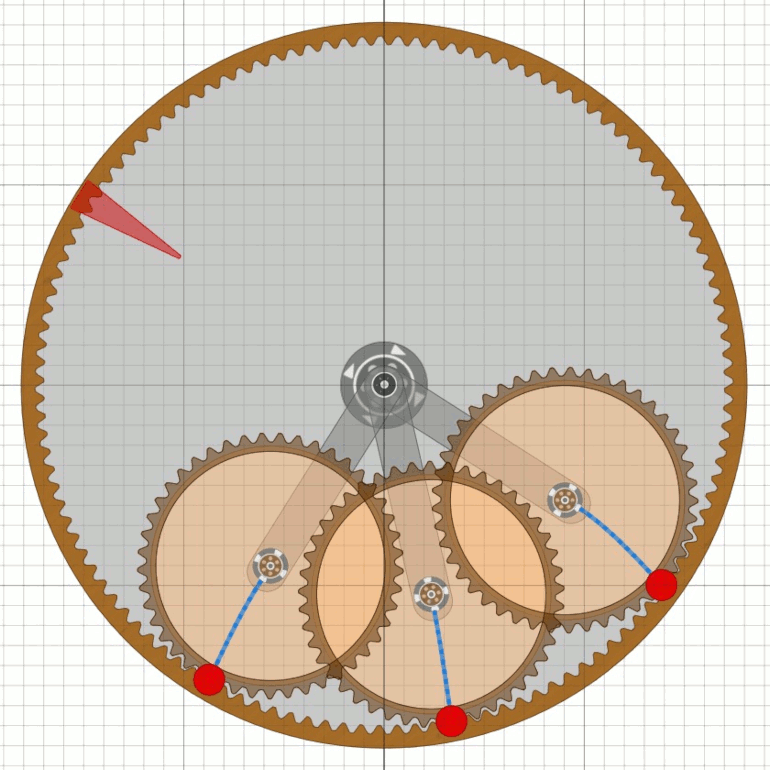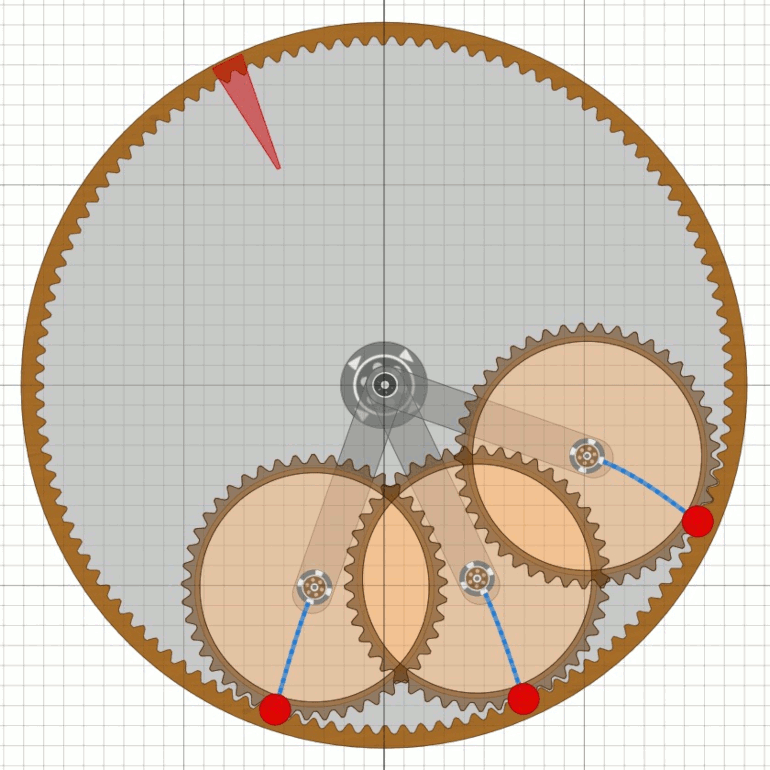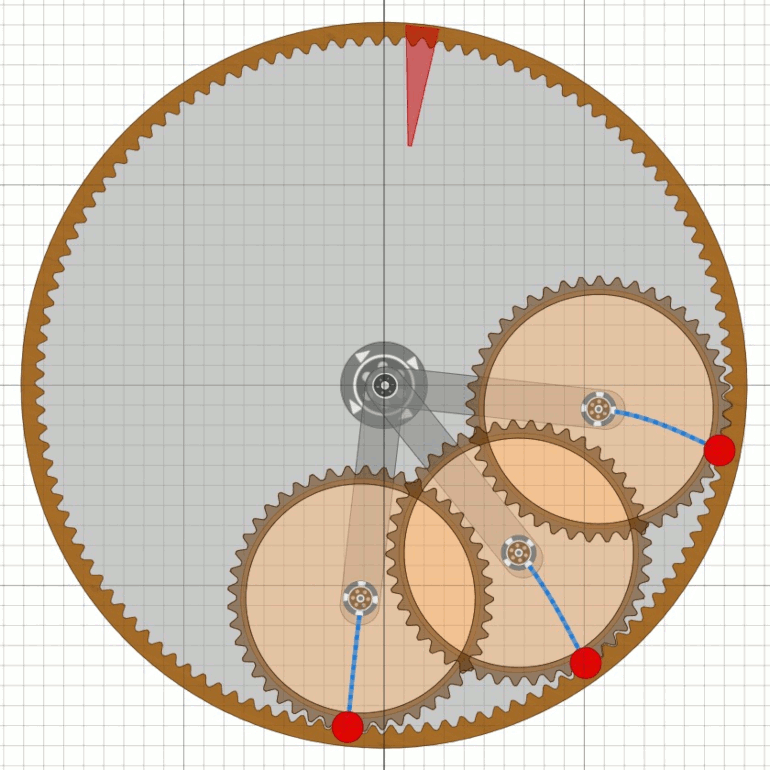
Das Stampfwerk der ersten Räder
Das Stampfwerk dient zum Anregen des Unwuchtsystems. Bei den ersten Rädern gibt es drei
doppelwirkende Stampfer, so dass pro Umdrehung der Achse sechs Impulse erzeugt werden. Unter der
Annahme, dass die Achse fest mit dem Rad verbunden ist, sollten also 6 Satelliten im Rad sein.
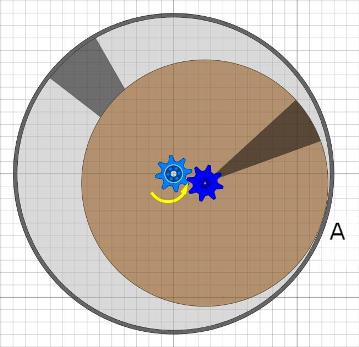
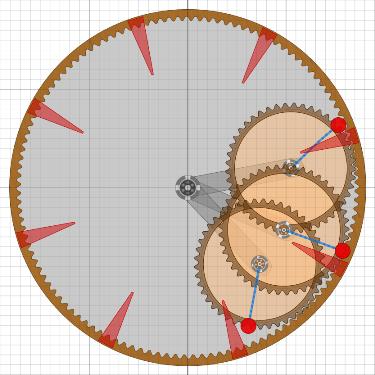
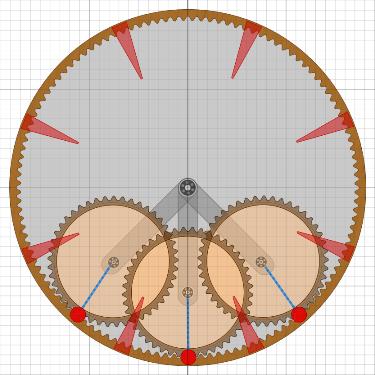
Überlegungen mit 5 Satelliten klammere ich hier erst einmal aus. Das Unwuchtsystem der ersten RäderDa bei den ersten Rädern die Radscheibe sehr dünn war, muss die Mechanik des Unwuchtsystems sehr einfach gewesen sein. Am wahrscheinlichsten erscheint mir aktuell eine Anordnung wie in der Animation mit sechs Satelliten nach MT18.
Es ist ein optimales Zusammenspiel von Pirouetten-Effekt und Fliehkraft.
Wenn das Fluggewicht unten (bei 6 Uhr) angekommen ist, so ist es durch
die Fliehkraft mehr als doppelt so schwer, wäre also nur mit viel Energie zu heben.
Durch den Antrieb des Satelliten wird das Gewicht stark abgebremst und
gleichzeitig die Feder gespannt. Der Schwung des Gewichts geht aber nicht verloren,
er beschleunigt über die Feder sogar das Rad indem die Welle des Satelliten
in Bewegungsrichtung gedrückt wird. Und weil die Fliehkraft jetzt weg ist, lässt
sich das Gewicht leichter anheben unter Mitwirkung des Pirouetten-Effekts.
Die Erkenntnis:
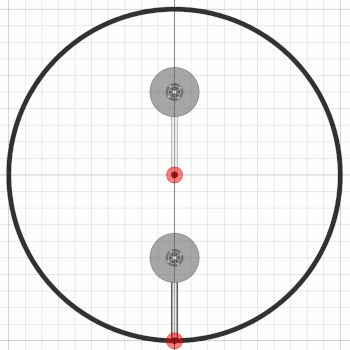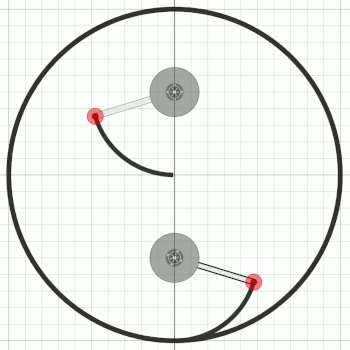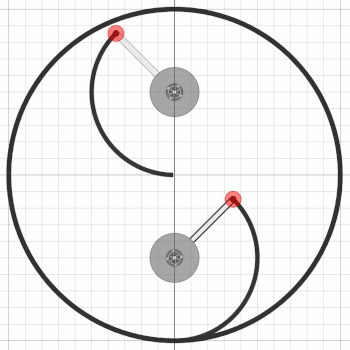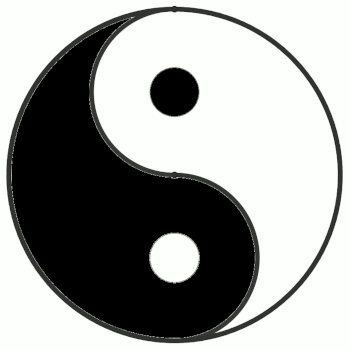
Zu diesem Unwuchtsystem schreibt Bessler in AP 81: Das Yin-Yang-Symbol
Und irgendwie habe ich hier eine Assoziation zum Yin-Yang-Symbol.
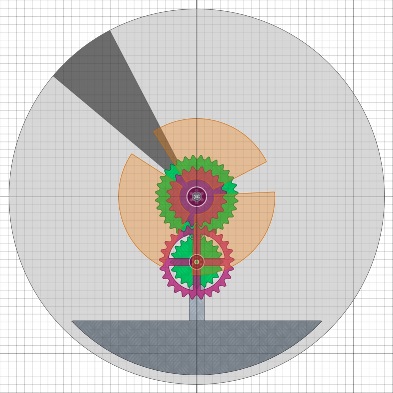
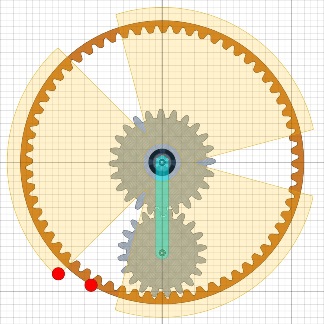
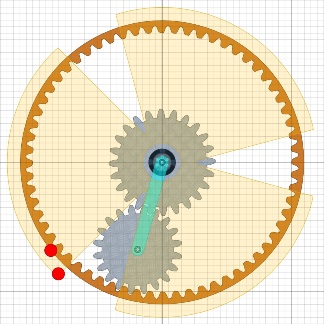
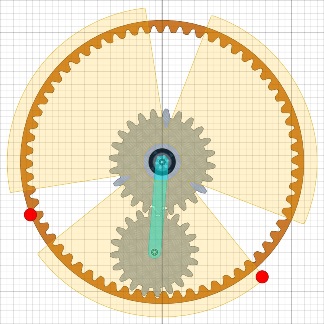
Das Geheimnis in der AchseBessler hatte keinen Elektromotor zum Antrieb des unteren Satelliten, also muss er es anders gemacht haben. Vielleicht hat er ja ein Reibrad benutzt, das zur richtigen Zeit das Satellitenrad gedreht hat. Das errinnert doch sehr an meine Interpretation der AP-Grafik vom April 2023, die ich gerne als Motus bezeichne („motus wheel” in der englisch-sprachigen Literatur).
Drehe ich jetzt meine Blender-Konstruktion aus der Draufsicht heraus, dann entsteht das Bild unten.
Zu beachten ist, dass die Reibräder die Drehung der Satelliten nur definiert
zu Ende bringen müssen. Zum Andrehen gibt es sicher zusätzlich einen Stift
oder eine Nocke, sonst wäre die Belastung der Reibräder zu groß.
Wie aber kann man eine Drehzahl verdoppeln ohne festen Punkt im Rad?
Und jetzt zum heikelsten Punkt im Bessler-Rad:
Was soll beim Eingriff eines Zapfen geschehen?
Meine Lösung für die Mechanik in der Achse sieht aktuell so aus:
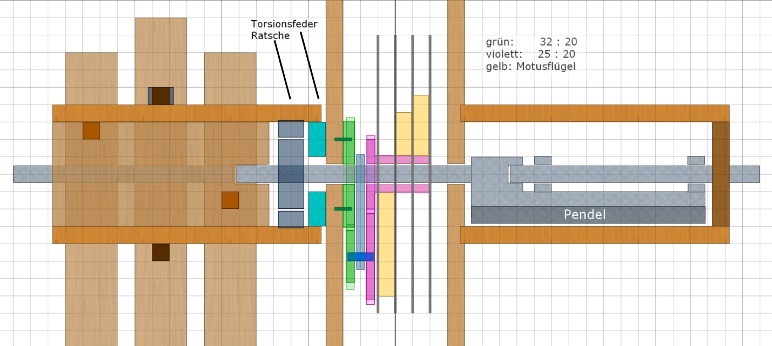
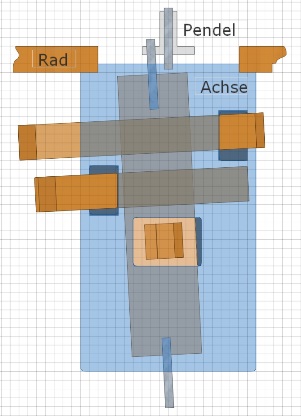
Das Bild skizziert den inneren Aufbau der Achse nach den Maßen des Draschwitz-Rades. Nur angedeutet ist die Ratsche in der linken Achse sowie die Torsionsfeder zum Rad. Die Trennscheiben zwischen den Motus-Flügeln sorgen dafür, dass nur der richtige Satellit gedreht wird. Der Platz links vom Motus ist für die sechs Riemen reserviert. Die Welle des Rades ist nicht durchgehend, da ja im Zentrum des Rades ein Teil der Welle mit dem Pendel schwingt. Die Welle ist also zwei mal unterbrochen, damit die äusseren Auflagezapfen sich mit dem Rad bzw. der Achse drehen können. Jetzt wirds schräg
Wer bis hierher noch folgen konnte, der hat vielleicht ein kleines Problem ent-deckt:
Beim Eingriff eines Stampfers gibt es einen starken Impuls auf den Zapfen und dieser
Impuls muss das Pendel zurückstoßen um das Ein- und Ausschwingen zu
beschleunigen. Aber kann das so funktionieren?
Man könnte es mit einem invertierenden Planetengetriebe lösen, also
Zapfen am Hohlrad (=äussere Achse), den Planetenträger mit dem Rad verbunden
und das Sonnenrad mit dem Pendel. Dann würde das Pendel zurück geschwungen
während das Rad sich weiter dreht, genau so wie gewünscht.
Und da kommt mir ein ganz „schräger” Gedanke. Könnte nicht ein
Zapfen direkt das Pendel auslenken? Dazu müsste das Pendel seitlich eine Nase
(Auflage, Öse) haben wo ein Gestänge vom Zapfen her eingreifen könnte.
Die Schrägstellung der zentralen Zapfenwelle beträgt etwa 4 Grad.
Der Hund ist wohl der gesamte Antrieb, das „primum movens”, vom Stampfer über die Zapfen bis zum Pendel auf der gegenüberliegenden Seite. Auf dem Bauche kriecht er durch das enge Rohr der einen Achse, da lässt er die Pfoten sehen, auf die dann die dürren Stampfer schlagen. Als Ergebnis wedelt der Schweif, das Pendel. Dieses Pendel bedient die inneren Maschinen. Es ist die Basis für die Zahnräder zum Motus hin und moduliert auch gleichzeitig dessen Geschwindigkeit. Das wesentliche Gewicht des Pendels liegt aber in der gegen-überliegenden Achse. Da die Pendelläge ja nur ca. 5 Zentimeter betragen darf, füllt es diese dann komplett aus, um genügend Masse zu bekommen.
Eine kleine Anmerkung noch zur Animation:
Damit ist das Prinzip der ersten zwei Räder geklärt. Das Prinzip der bidirektionalen Räder
Nachdem wir das Prinzip der ersten Räder zumindest in der Theorie geklärt
haben, sollte es doch auch für die bidirektionalen Räder klappen
von denen es ja sogar Stiche und Beschreibungen von Bessler gibt.
Doch die bidirektionalen sind noch um einiges komplexer und über ihre Funktion
ist von Bessler auch sehr wenig herauszukriegen. Nur solche Hinweise wie in
PA 66 wo er das Merseburger dem Draschwitzer Rad gegenüber stellt
und von letzterem schreibt: Belegt sind folgende Eigenschaften:
Von mir als sehr wahrscheinlich zusätzlich angenommen:
Das Unwuchtsystem der bidirektionalen Räder
Die Animation zeigt die Mechanik des Hubsystems für ein Fluggewicht
Den Antrieb in der Animation übernimmt ein Motor in der Achse des Satellitenrades.
Winkelabhängig wird der Motor kurz eingeschaltet, nach ca. 45° Rad-Drehung
folgt der Freilauf und kurz vor dem Einrasten wird die Satelliten-Drehung abgebremst.
Das Hochschwingen geht sehr schnell. Die Energie dafür kommt aus der Trägheit
des Rades, dem Gewicht von 2 Unwuchtsystemen, dem Kick von einem Stampfer
und evtl. von einem Pendel und einem Schwungrad.
Achtung: Weitere Simulationen geben Anlass zu der Vermutung, dass die 8 Rasten
nicht nur nicht vorhanden waren, sondern sogar schädlich gewesen wären.
Sie wurden hier nur noch zur besseren Visualisierung dargestellt.
Damit wird aber auch klar, weshalb hier keine Filzauflagen notwendig waren.
Das Stampfwerk der bidirektionalen Räder
Beim Stampfwerk gibt es jetzt eine Kuriosität. Läuft das Rad wie gewohnt im Uhrzeigersinn cw,
so ist alles normal. Das Stampfwerk dreht sich in die gleiche Richtung wie das Rad, auch cw.
Läuft das Rad aber gegen den Uhrzeigersinn ccw, dann muss das Stampfwerk trotzdem
cw laufen, sonst würde es blockieren. Diese Umschaltung muss beim Starten des Rades
automatisch erfolgen. Das Geheimnis in der Achse
Das Geheimnis in der Achse der bidirektionalen Räder ist noch nicht ganz gelöst.
Ich will hier aber den Startvorgang kurz darstellen, damit man daraus evtl. mal eine
geeignete Mechanik ableiten kann. Wir beginnen also mit dem Rad im Stillstand, siehe oben,
und drehen das Rad langsam cw. Jetzt nehmen wir an, dass ein Motus-Flügel
am linken Satelliten anliegt und diesen nach rechts wegdreht.
Dadurch geht auch das Fluggewicht nach oben.
Solange dieses seine höchste Position nicht erreicht hat,
ist der Vorgang reversibel, d.h. das Rad wird sich zurückdrehen, wenn wir es loslassen.
Und das sagt uns Bessler wohl im Gründlichen Bericht auf Seite 16:
Angetrieben werden die Satelliten wie bei den ersten Rädern vom sog. Motus,
allerdings dreht sich dieser jetzt nicht cw und zweimal so schnell wie das Rad,
sondern ccw und 8/3-mal so schnell. Das Getriebe hierzu ist sogar einfacher als
bei den ersten Rädern. Vom äusseren Zahnkranz ausgehend könnte man
die gewünschte Drehzahl mit zwei Zahnrädern erreichen.
Bis hierher ist das Ganze recht überschaubar und läuft auch bidirektional.
... Fortsetzung folgt ! Erwartbare Leistung
Es wird vielfach angenommen, dass ein Bessler-Rad nur eine sehr geringe Leistung abgeben kann
und deshalb keine Lösung für unser Energieproblem sein wird.
Ich bin da ganz anderer Meinung.
Beim Bessler-Rad wird das ähnlich sein, wenn auch die Energiedichte niedriger ist.
Man wird also von kleinen Maschinen keine großen Leistungen erwarten können,
aber man kann wohl sehr große Maschinen bauen, die dann auch entsprechende Leistungen
abgeben können. Woher kommt die Energie?
Wenn ich gefragt werde, woher eigentlich die Energie für ein Bessler-Rad kommen soll,
so sage ich immer, „die kommt aus der Schwerkraft” - siehe swing-by-Manöver.
Das will ich hier noch genauer erklären, soweit ich das physikalisch verstanden habe.
Wegunabhängigkeit der Arbeit
Was ist jetzt bei einem swing-by-Manöver anders?
Ich will mich da jetzt nicht weiter einlassen, das sollten eigentlich langsam die Physiker
machen, die davon was verstehen. Meine Äthertheorie
Nach der sog. etablierten Physik von heute kann so ein Bessler-Rad (noch) nicht funktionieren, der
Energie-Erhaltungs-Satz „verhindert” das. Bei vielen Studien („global scaling” von Prof. Dr. Hartmut Müller, den Schriften von Prof. Kanarev, den Seiten von Prof. Alfred Evert, von Gabi Müller usw.) konnte ich erfahren wie begrenzt doch das Wissen der heutigen Physik ist und wie da getrickst und postuliert wird. Meine Äthertheorie fand ich auf den Seiten von Prof. Alfred Evert im Internet, die nach seinem Tod leider nur noch bruchstückhaft im Archiv zu finden sind. Er hat sich mit seinen Ausführungen zwar oft „vergaloppiert”, aber er hat eine Äthertheorie ins Leben gerufen, die ich in mein „Wissenspuzzle” voll integriert habe. Ich gebe zu, dass es Monate gedauert hat bis ich diese Theorie mit meinem übrigen Wissen vereinbaren konnte, aber jetzt kann ich es mir nicht mehr anders vorstellen. Diese Erkenntnis widerspricht anfangs allem bisher Gelernten so dramatisch, dass man sich wirklich erstmal darauf einlassen und von Grund auf neu denken muss. Das ist vielleicht ähnlich wie wenn ein Katholik die Reinkarnation in seinen Glauben aufnehmen will.
Was also ist jetzt diese Äthertheorie?
Mit dem sog. Urknall sind wir schlagartig aus dem Zentralschlauch aufgetaucht
und seitdem dehnt sich „für uns” der Raum aus. Dazu braucht es keine
dunkle Energie, keine dunkle Materie oder sonst ein Hirngespinst.
Hier noch ein kleines Beispiel wie uns die heutigen Physiker ein X für ein U
vormachen wollen: beim Photon.
Prof. Kanarev hat schon vor vielen Jahren das Photon richtig erfasst indem er ausschließlich aufgrund von Formeln, die das Photon beschreiben, die richtige Form und seine Ausmaße berechnet hat. Und das ist mit der Äthertheorie absolut vereinbar und erklärt auch die Polarisation des Lichts. Danach ist das Photon ein sechseckiger Ring, der mit Lichtgeschwindigkeit durch den Äther „rollt”.
Und der Welle/Teilchen-Dualismus wird uns auch immer wieder vor die Nase gehalten, den man in der Wissenschaft
immer noch nicht aufklären kann. Das Photon ist nie ein Teilchen, es ist nur eine spezielle Form
von Ätherschwingung, die von Physikern in ihren Versuchen mit anderen Formen von Ätherschwingungen
(Kanten und Spalten) in „Reaktion” gebracht wird. Bei großem Spalt fliegt das Photon einfach
durch, bei kleinem Spalt interagiert das eine mal mit der einen Kante und das andere mal mit der anderen und
so ergibt sich das bekannte Beugungsmuster.
Impressum - für diese Seiten ist verantwortlich: |